
돈이 미래에 얼마나 불어날지 궁금하신가요? 아니면 지금 당장 얼마를 투자해야 미래에 원하는 금액을 만들 수 있을지 고민되시나요? 그렇다면 잘 오셨습니다! 마치 마법의 수정 구슬처럼 미래 재정을 예측하는 엑셀의 PV 함수와 FV 함수, 오늘 제대로 파헤쳐 보겠습니다. 복잡한 계산은 엑셀에게 맡기고, 여러분은 느긋하게 커피 한 잔의 여유를 즐기세요! 😉 이 글에서는 PV 함수와 FV 함수의 활용법을 다양한 실전 예제를 통해 알려드리고, 헷갈리기 쉬운 부분과 흔히 발생하는 오류와 해결책까지 쏙쏙 짚어드릴 예정입니다. 자, 이제 엑셀 마법사가 되어 미래를 설계해 볼까요? ✨
예제파일은 아래 내려보시면 있으니 다운받아서 활용해보세요.
PV 함수 이해하기
자, 엑셀의 재무 함수계의 숨은 보석, PV 함수! 드디어 베일을 벗을 시간입니다! 두근두근?! 😎 이 녀석, 얼핏 보면 좀 복잡해 보일 수 있는데요, 사실 원리만 알면 껌이랍니다! (진짜예요! 믿으세요!)
PV 함수, Present Value의 약자로, 미래에 받을 돈의 현재 가치를 계산해주는 아주 똑똑한 친구랍니다. "아니, 미래에 받을 돈의 *현재* 가치라니?! 시간 여행이라도 하나요?!" 라고 생각하실 수도 있겠죠? 맞습니다! 시간 여행은 못하지만, 돈의 시간 여행은 가능하게 해주는 마법같은 함수랄까요? ✨
돈은 시간이 지남에 따라 가치가 변동하잖아요? 예를 들어, 지금 당장 100만원을 받는 것과 1년 후에 100만원을 받는 것은 다르죠! 1년 후에 받는 100만원은 지금 당장 받는 100만원보다 가치가 낮습니다. 왜냐? 인플레이션, 투자 기회 등등 여러 요소가 있기 때문이죠! 이런 미묘하고 복잡한 계산을 PV 함수가 깔끔하게 해결해준답니다. 👏👏👏
PV 함수의 기본 구조
자, 그럼 이 마법의 함수, 어떻게 사용하는 걸까요? PV 함수의 기본적인 구조는 다음과 같습니다.
PV(rate, nper, pmt, [fv], [type])
뜨악! 갑자기 영어가 튀어나와서 당황하셨나요? 걱정 마세요! 하나씩 차근차근 설명해드리겠습니다. 😉
PV 함수 인자 설명
- rate: 이자율(할인율)입니다. 쉽게 말해, 돈의 시간 여행에 필요한 연료 같은 거죠! 연간 이자율을 사용하며, 만약 이자 지급 기간이 월별이라면 연 이자율을 12로 나눠서 입력해야 합니다. 0.05, 0.1처럼 소수로 입력하는 것도 잊지 마세요!
- nper: 납입 기간의 총 횟수입니다. 돈의 시간 여행 기간이라고 생각하면 쉽겠죠? 만약 매달 납입한다면, 납입할 년수에 12를 곱해야 합니다. 예를 들어 3년 동안 매달 납입한다면 nper는 36이 됩니다.
- pmt: 각 기간에 지급할 금액입니다. 매 기간 일정한 금액을 지급한다면 음수로 입력하고, 일정한 금액을 받는다면 양수로 입력합니다. (꿀팁! 대출 상환액을 계산할 때는 음수로 입력해야 한답니다!)
- [fv]: 미래 가치입니다. 선택적으로 입력할 수 있는 부분인데요, nper 기간 후에 받고 싶은 금액을 입력합니다. 예를 들어, 5년 후에 1억 원을 모으고 싶다면, fv에 100,000,000을 입력하면 됩니다. 만약 생략하면 0으로 간주됩니다.
- [type]: 납입 시점을 나타냅니다. 이것도 선택적으로 입력할 수 있는데요, 0은 기간 말에 납입(후불), 1은 기간 초에 납입(선불)을 의미합니다. 만약 생략하면 0으로 간주됩니다. (세상에… 디테일 좀 보세요! 👍)
PV 함수 활용 예시

자, 이제 실제 예시를 통해 PV 함수를 더 자세히 알아볼까요? 예를 들어, 연 이율 5%로 3년 동안 매달 10만 원씩 투자했을 때, 현재 가치는 얼마일까요?
=PV(B5/100/12, C5*12,-A5)
결과값은 약 3,336,570가 나옵니다. 이는 현재 시점에서 3년 동안 매달 10만 원씩 투자하는 것이 현재 약 3,336,570원의 가치가 있다는 것을 의미합니다. (오… 신기방기! 🤩)
PV 함수, 이제 좀 감이 잡히시나요? 처음엔 어려워 보여도 몇 번 사용해 보면 금방 익숙해질 거예요! 다음에는 더욱 강력한 FV 함수에 대해 알아보겠습니다! 기대해주세요! 😉 (커밍 쑨~!)
각 함수 사용법은 예제 파일을 다운로드해서
👇👇👇직접 변경해가면서 사용해보세요👇👇👇
FV 함수 활용 시나리오
자, 이제 엑셀의 마법 같은 함수, FV 함수의 활용 시나리오를 탐험해 볼 시간입니다! 마치 RPG 게임에서 새로운 스킬을 배우는 것처럼 흥미진진하지 않나요?! FV 함수는 미래 가치를 계산하는 함수인데요, 이게 얼마나 유용한지 알면 깜짝 놀라실 겁니다! 마치 마법 지팡이처럼 휘두르면 돈이 뿅! 하고 나타나는 건 아니지만요… (아쉽죠?^^) 하지만 미래를 예측하는 데는 이만한 도구가 없답니다!
시나리오 1: 꿈★은 이루어진다! - 내 집 마련 프로젝트
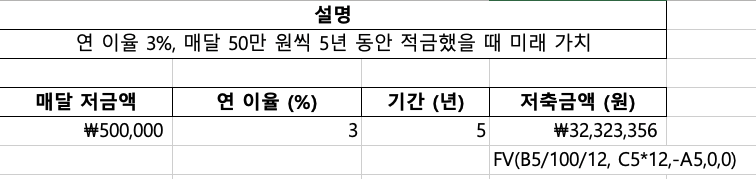
30세의 빛나는 청춘, 김철수 씨는 내 집 마련의 꿈을 이루기 위해 저축을 시작했습니다. 매달 50만 원씩 5년 동안 연이율 3%로 적금한다면 만기 시 얼마를 받을 수 있을까요? FV 함수를 사용하면 간단하게 계산할 수 있답니다!
* FV(rate, nper, pmt, [pv], [type])
* FV(3%/12, 5*12, -500000, 0, 0) = 약 32,323,356원
와우! 5년 후면 약 3천만 원이 넘는 목돈이 생긴다니?! 김철수 씨, 꿈에 그리던 내 집 마련이 눈앞에 보이는 듯합니다! 축하드려요! (짝짝짝!)
시나리오 2: 💰💰💰 투자의 귀재?! - 주식 투자 시뮬레이션
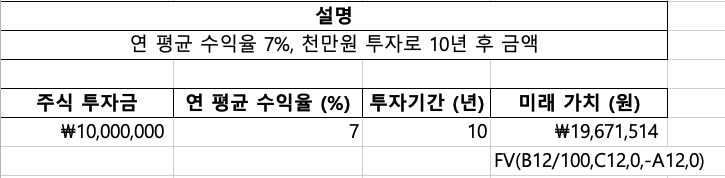
주식 투자에 관심이 많은 박영희 씨는 현재 1,000만 원을 투자했습니다. 연평균 수익률이 7%라고 가정할 때, 10년 후 그녀의 투자금은 얼마나 불어나 있을까요? 궁금하시죠?! FV 함수가 답을 알려드립니다!
* FV(rate, nper, pmt, [pv], [type])
* FV(7%, 10, 0, -10000000, 0) = 약 19,671,514원
대박! 10년 후면 투자금이 거의 두 배가 된다니?! 역시 꾸준한 투자는 마법과 같군요! (물론, 실제 주식 투자는 변동성이 크니 주의해야 합니다!)
시나리오 3: 미래를 위한 준비! - 자녀 학자금 마련 계획
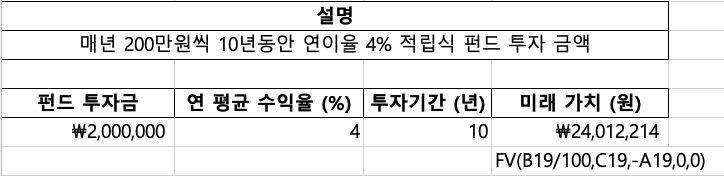
사랑하는 자녀의 미래를 위해 교육 자금 마련은 필수죠! 5살 딸아이를 둔 이지혜 씨는 매년 200만 원씩 10년 동안 연이율 4%로 적립식 펀드에 투자할 계획입니다. 10년 후 딸아이가 대학교에 입학할 때쯤 얼마의 학자금이 모여 있을까요?
* FV(rate, nper, pmt, [pv], [type])
* FV(4%, 10, -2000000, 0, 0) = 약 24,012,214원
와우! 이지혜 씨의 딸은 든든한 지원을 받으며 대학 생활을 시작할 수 있겠네요! 역시 미리미리 준비하는 것이 최고입니다! (엄지 척!)
시나리오 4: 은퇴 후 걱정 끝! - 연금 계획 세우기
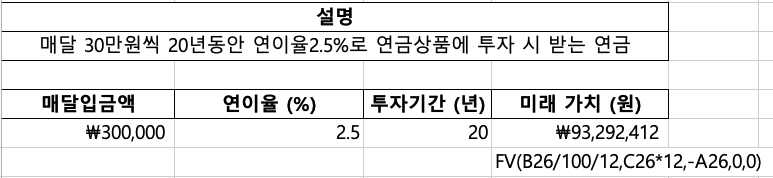
은퇴 후에도 여유로운 삶을 즐기고 싶은 최민수 씨는 매달 30만 원씩 20년 동안 연이율 2.5%로 연금 상품에 투자할 계획입니다. 과연 20년 후에는 얼마의 연금을 수령할 수 있을까요? FV 함수가 알려드립니다!
* FV(rate, nper, pmt, [pv], [type])
* FV(2.5%/12, 20*12, -300000, 0, 0) = 약 93,292,412원
놀랍습니다! 20년 후에는 거의 1억 원에 가까운 목돈이 마련된다니! 최민수 씨, 은퇴 후에도 걱정 없이 행복한 삶을 누리실 수 있겠네요!
시나리오 5: 사업 확장의 꿈! - 투자금 회수 예측
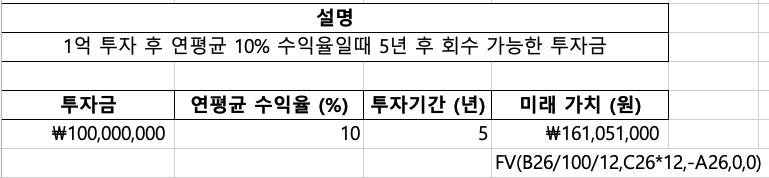
새로운 사업 아이템에 1억 원을 투자한 정미영 씨. 연평균 10%의 수익을 예상하고 있습니다. 5년 후 투자금 회수는 어떻게 될까요?
* FV(rate, nper, pmt, [pv], [type])
* FV(10%, 5, 0, -10000000, 0) = 약 161,051,000원
5년 후 1억 6천만 원 이상의 수익을 기대할 수 있다니! 정미영 씨의 사업 대박을 기원합니다! (짝짝짝!)
이처럼 FV 함수는 다양한 상황에서 미래 가치를 예측하는 데 유용하게 활용될 수 있습니다. 이제 여러분도 FV 함수 마스터가 되어 미래를 설계해 보세요! 어때요, 참 쉽죠?! 😉
흔히 발생하는 오류와 해결책
PV, FV 함수! 참 편리하죠? 마치 마법처럼 숫자 몇 개 넣으면 미래 가치 뚝딱! 현재 가치 짠! 하고 나타나니까요. 그런데… 마법에도 함정은 있는 법! 가끔 예상치 못한 오류 때문에 머리를 쥐어뜯게 되는 경우가 있죠? 😫 "내가 뭘 잘못했지?!" 싶어 엑셀 창을 노려보게 되는 그 순간! 걱정 마세요! 여러분의 엑셀 구원 요정이 여기 있습니다! ✨ 지금부터 PV, FV 함수를 사용할 때 흔히 발생하는 오류와 그 해결책을 아주 쉽고 재밌게 알려드릴게요! 😉
#NUM! 오류
"아니, 숫자만 넣었는데 왜 #NUM! 오류가 뜨는 거야?!" 라고 외치고 싶으신가요? 범인은 바로 숫자처럼 보이지만 사실은 텍스트인 녀석일 가능성이 높습니다! 🕵️♀️ 예를 들어, 숫자 앞에 공백이 있거나, 쉼표(,) 대신 점(.)을 사용했을 때 이런 오류가 발생할 수 있어요. 숫자 서식이 제대로 적용되었는지, 혹시 텍스트로 입력된 숫자가 있는지 꼼꼼히 확인해 보세요! 🧐
#VALUE! 오류
PV, FV 함수는 숫자만 좋아합니다! 🍎 만약 날짜, 텍스트 등 숫자가 아닌 값을 인수로 입력하면 #VALUE! 오류가 딱! 하고 나타나죠. 특히 이자율(rate)이나 기간(nper)에 텍스트가 들어가는 경우가 많으니 주의하세요! 👀 마치 사과 바구니에 오렌지를 넣으려고 하는 것과 같답니다. 🍊 각 인수에 알맞은 유형의 값을 입력해야 함수가 제대로 작동할 수 있어요!
예상과 다른 결과
PV, FV 함수는 현금 흐름의 방향을 고려합니다! 💸 돈이 들어오는 경우(+)와 나가는 경우(-)를 구분해야 정확한 결과를 얻을 수 있죠. 예를 들어, 대출을 받는 경우 현재 가치(PV)는 양수(+)이지만, 대출금을 상환하는 경우 미래 가치(FV)는 음수(-)가 되어야 합니다. 마치 시소처럼 균형을 맞춰야 원하는 결과를 얻을 수 있다는 사실! ⚖️ 부호를 잘못 입력하면 전혀 엉뚱한 숫자가 나올 수 있으니, 현금 흐름의 방향을 명확하게 파악하고 부호를 정하는 것이 중요해요!
복잡한 계산?
불규칙적인 현금 흐름 때문에 머리가 지끈거린다면? 🤯 NPV나 XNPV 함수를 사용해 보세요! 이 함수들은 서로 다른 시점에 발생하는 현금 흐름의 현재 가치를 계산해줍니다. 마치 복잡한 미로를 헤쳐나가는 데 필요한 지도와 나침반 같은 역할을 해준답니다! 🧭 NPV는 기간이 일정한 경우, XNPV는 기간이 불규칙적인 경우에 사용하면 돼요!
엑셀 버전 차이
혹시 다른 사람이 만든 엑셀 파일을 열었는데 함수가 제대로 작동하지 않나요? 🤔 엑셀 버전에 따라 함수의 인수나 기능이 조금씩 다를 수 있습니다! 마치 같은 언어라도 사투리가 있는 것처럼요! 🗣️ 사용하는 엑셀 버전에 맞는 함수 설명서를 참고하여 인수를 정확하게 입력해야 합니다.
소수점 이하 자릿수
때로는 너무 많은 소수점 이하 자릿수 때문에 눈이 핑핑 돌 수도 있죠? 😵 이럴 때는 ROUND 함수를 사용하여 원하는 자릿수로 반올림하면 깔끔하게 표시할 수 있습니다! 마치 정원사가 잔디를 깔끔하게 다듬는 것처럼요! 🌱 ROUND 함수는 반올림할 숫자와 소수점 이하 자릿수를 인수로 받습니다.
숨겨진 오류 찾기
가끔은 엑셀이 수식을 자동으로 계산하지 않아 오류가 발생하는 경우도 있습니다. 🤫 이럴 때는 수식 탭에서 계산 옵션을 "자동"으로 설정해야 실시간으로 계산 결과가 업데이트됩니다. 마치 자동차 엔진처럼 엑셀도 켜져 있어야 제대로 작동하겠죠? 🚗
오류 메시지 활용
엑셀은 오류가 발생했을 때 친절하게(?) 오류 메시지를 보여줍니다. 💬 이 메시지는 오류의 원인을 파악하는 데 중요한 단서가 되므로, 무시하지 말고 꼼꼼히 읽어보세요! 마치 탐정이 범인을 찾기 위해 단서를 수집하는 것처럼 말이죠! 🔎
자, 이제 PV, FV 함수 정복을 위한 만반의 준비가 되었나요? 💪 이 팁들을 잘 활용하면 더 이상 오류 때문에 고생할 필요 없이 엑셀 마법사가 될 수 있을 거예요! ✨ 그럼, 즐거운 엑셀 탐험 되세요! 🚀
실전 예제로 배우는 PV, FV 함수
자, 이제 드디어!! 엑셀 PV, FV 함수를 가지고 놀아볼 시간입니다! 지금까지 이론만으론 좀 답답하셨죠?! 걱정 마세요! 제가 준비한 실전 예제를 통해 PV, FV 함수의 매력에 퐁당~ 빠지실 겁니다! ^^ 마치 마법처럼 숫자들이 춤을 추는 모습을 볼 수 있을 거예요!
예제 1: 로또 당첨! 10억 받는 방법?! (PV 함수)
두둥! 드디어 로또 1등에 당첨되셨습니다!! 축하드립니다! 🎉🎉 10억 원이라는 어마어마한 금액! 하지만 일시불로 받을지, 연금처럼 20년 동안 나눠 받을지 고민이시라고요? 🤔 바로 이럴 때 PV 함수가 필요합니다!
- 연금 수령: 매년 5천만 원씩 20년 동안 받는다고 가정해 봅시다. 이자율은 연 3%라고 할게요. 과연 현재 가치는 얼마일까요? PV 함수를 사용하면 간단하게 계산할 수 있습니다!
=PV(3%, 20, -50000000)결과는 약 6억 7천만 원 정도! 어라? 10억보다 적네?! 이자의 마법 때문이죠! - 일시불 수령: 지금 당장 10억을 받는다면 현재 가치는… 당연히 10억 원이겠죠?! 굳이 PV 함수를 쓸 필요도 없어요! 😎
자, 이제 선택은 당신의 몫! 일시불로 10억을 받을지, 아니면 매년 5천만 원씩 20년 동안 나눠 받을지… PV 함수 덕분에 현명한 선택을 할 수 있겠죠?! 😉
예제 2: 내 집 마련의 꿈! (FV 함수)
열심히 저축해서 5년 뒤 내 집 마련을 하고 싶으신가요? 🏡 매달 얼마씩 저축해야 목표 금액을 달성할 수 있을지 궁금하시다고요? FV 함수가 당신의 꿈을 현실로 만들어 드립니다! ✨
- 목표 금액: 3억 원
- 저축 기간: 5년 (60개월)
- 연이율: 2.5% (월이율로 환산하면 약 0.21%)
=FV(0.21%, 60, -저축액) 이 공식에서 저축액을 조정해가며 목표 금액인 3억 원에 도달할 때까지 계산해 보세요! 매달 약 470만 원 정도를 저축하면 5년 뒤 3억 원을 모을 수 있습니다! (물론 이자율 변동에 따라 결과는 달라질 수 있어요!)
예제 3: 사업 투자, 대박 날까? (NPV 함수)
새로운 사업 아이템을 발견하셨다고요?! 💰 투자할 가치가 있는지 궁금하시죠? 이럴 땐 NPV 함수 (Net Present Value, 순현재가치) 가 정답입니다!
- 초기 투자금: 1억 원 (마이너스(-) 값으로 입력해야 합니다!)
- 1년 후 예상 수익: 3천만 원
- 2년 후 예상 수익: 5천만 원
- 3년 후 예상 수익: 7천만 원
- 할인율: 5% (투자에 대한 기회비용 등을 고려한 비율입니다.)
=NPV(5%, 30000000, 50000000, 70000000) - 10000000 계산 결과가 양수라면 투자 가치가 있다는 뜻! 음수라면… 다시 한번 생각해 보시는 게 좋겠죠? 😅
예제 4: 변동 이자를 고려한 미래 가치 계산 (FVSCHEDULE 함수)
이자율이 변동된다면?! FVSCHEDULE 함수를 사용해 보세요! 예를 들어, 3년 만기 적금에 1억 원을 예치하는데, 첫해 이자율은 2%, 둘째 해는 2.5%, 셋째 해는 3%라고 가정해 봅시다.
=FVSCHEDULE(10000000, {0.02, 0.025, 0.03}) 이렇게 입력하면 변동 이자율을 적용한 미래 가치를 계산할 수 있습니다! 참 쉽죠?! 😉
더 재미있는 예제는 없나요?!
물론입니다! 세상에는 숫자만큼이나 다양한 예제들이 존재합니다! 여러분의 상상력을 발휘해서 PV, FV 함수를 다양하게 활용해 보세요! 부동산 투자, 주식 투자, 연금 계획 등… PV, FV 함수는 여러분의 금융 생활에 든든한 조력자가 되어줄 것입니다! 😊 이제 엑셀 마법사가 되어 숫자의 세계를 정복해 보세요! 🧙♂️✨
자, 이제 PV와 FV 함수 정복의 길, 드디어 종착역에 다다랐습니다! 복잡해 보였던 함수들이 이제는 친숙하게 느껴지지 않으신가요? 마치 엑셀 시트 위에서 현금 흐름이 춤추는 모습이 눈앞에 그려지는 것 같죠? 😉 혹시 아직도 조금 헷갈리신다고요? 괜찮습니다! 처음부터 완벽한 사람은 없으니까요. 연습만이 살길입니다! 이 포스팅이 여러분의 엑셀 재무 관리 실력 향상에 조금이라도 도움이 되었기를 바라며, 저는 이만 물러가겠습니다. 다음에 더 재미있는 엑셀 팁으로 돌아올게요! 뿅! ✨
'엑셀 파보자' 카테고리의 다른 글
| 엑셀 RATE 함수 활용방법 및 오류해결방법 (0) | 2025.02.27 |
|---|---|
| 엑셀 PMT 함수 활용방법 및 오류해결방법 (0) | 2025.02.27 |
| 엑셀 재무 함수 정리 (0) | 2025.02.26 |
| 엑셀 DAVERAGE 함수 활용방법 및 오류해결방법 (0) | 2025.02.25 |
| 엑셀 DCOUNT 함수 활용방법 및 오류해결방법 (0) | 2025.02.25 |



